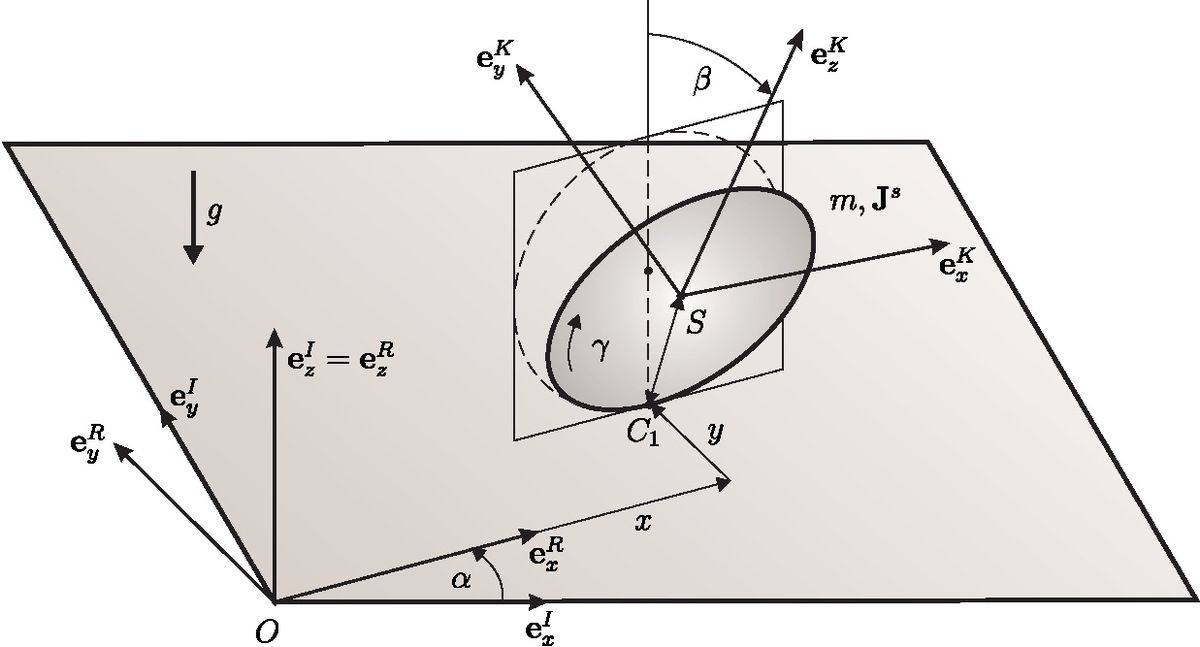
Regularization of Nonholonomic Constraints in Multibody Systems
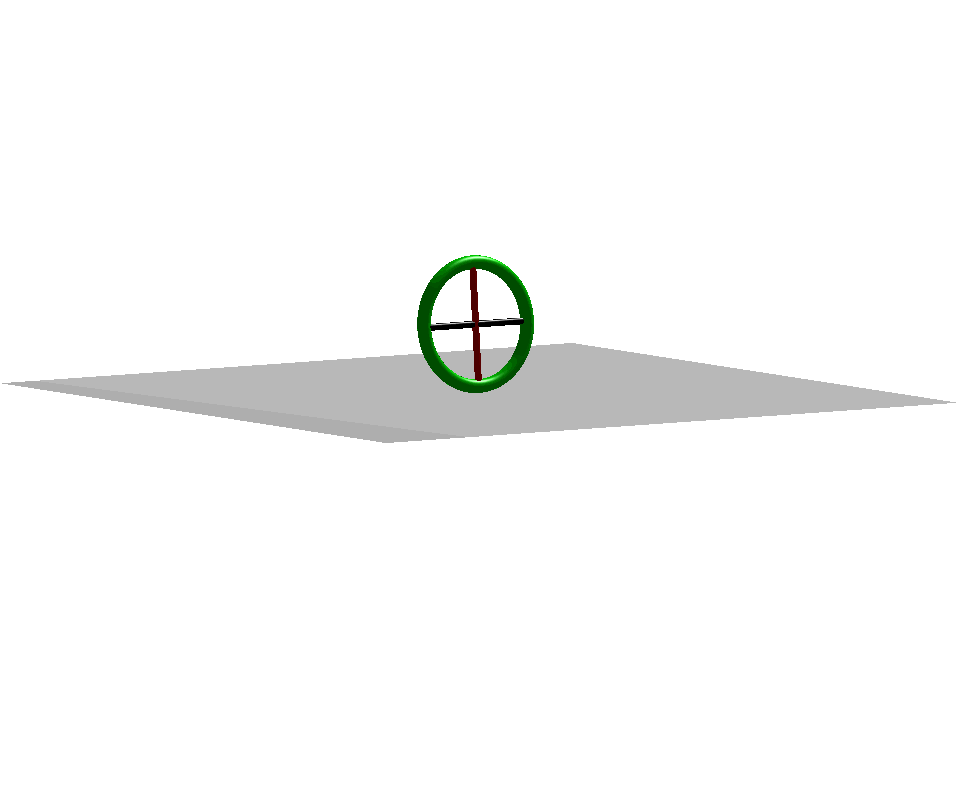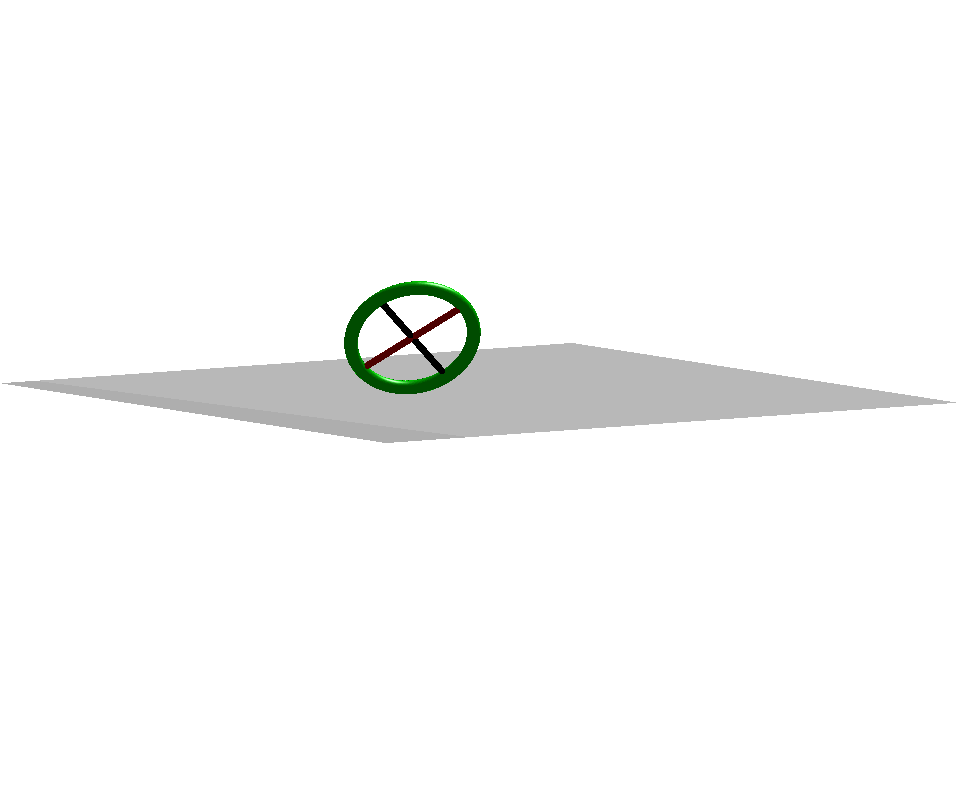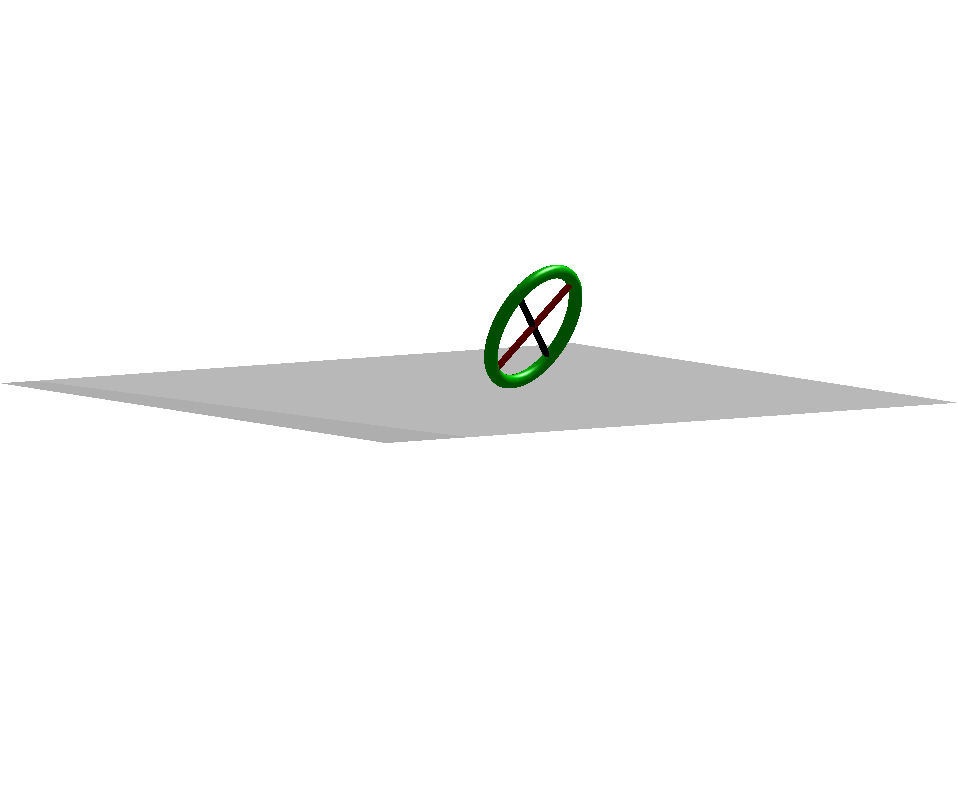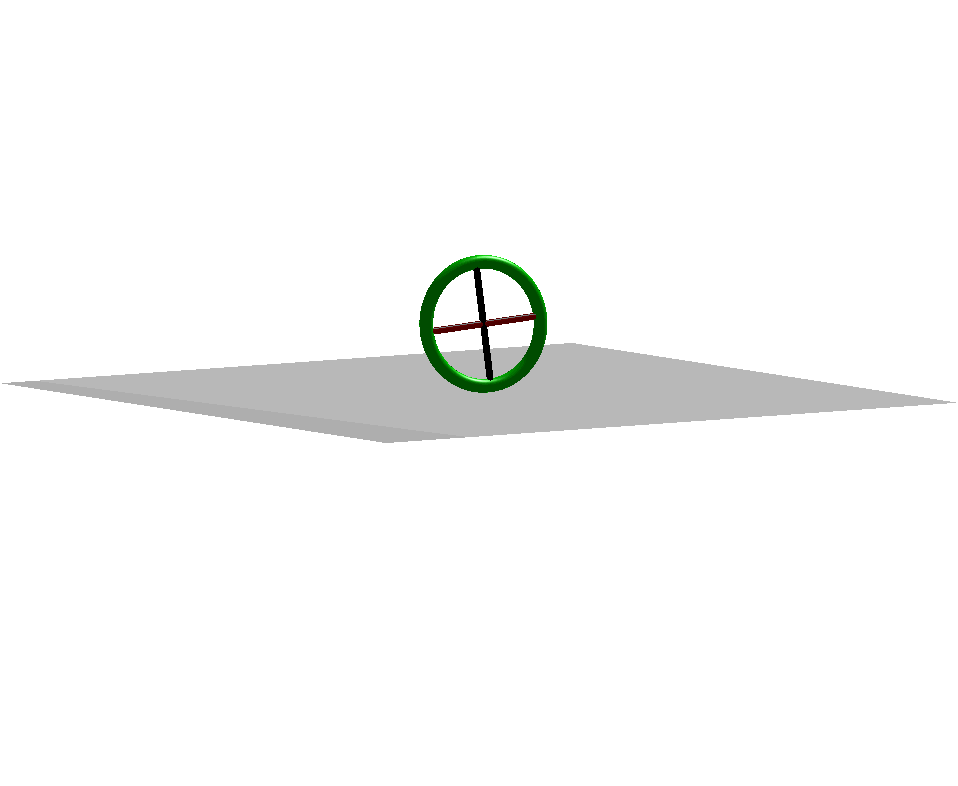
Rolling contacts are usual in various technical systems. Gear wheels in gearboxes, the motion of rolling elements in roller bearings or the Euler disk can be mentioned here as examples. Even the sliding of a clutch disk on an elastic support can become unstable transitioning into a rolling motion. In most cases rolling motion conditions yield non- holonomic constraint equations. Usually the non-holonomic constraints can be incorporated by the method of Lagrange multipliers. This formulation leads to index-2 differential algebraic problems. Different regularization approaches have been developed for higher index DAEs because of the numerical drift problems inherent for usual ODE methods. In the present paper we investigate a new regularization method that is motivated by physical considerations. Pure rolling is equal to “sticking” with a kinematically repositioned contact point. Usually sticking is modeled by introducing elasticity in the contact. Although constraints are mainly enforced by the elasticity in that case and the dissipative terms are necessary in order to avoid numerical oscillations in the contact. A suitable choice of the order of magnitude of the dissipative forces enhances the numerical performance of the method. The purpose of this kind of regularization is to get a consistent description for sliding, sticking and rolling contacts. Stamm applied this kind of regularization to a tangential contact law, extending the classical laws of friction to distributed contacts, where the problem of indeterminacy in the sticking state is circumvented by regularization. It this work we prove the convergency of the spring-damper regularization for the so called principal damping, which is motivated by the critical damping in the linear case, and the strong damping which is of the same magnitude order as the contact stiffness.
Contact: Prof. A. Fidlin, J. Deppler
| Title | Type | Graduand |
|---|---|---|
| Auslegung eines Prüfstandskozepts zur Abbildung verbrennungsinduzierter Schwungraddynamik | Masterarbeit |
Philipp Mall |
| Numerische Methoden für Mehrkörpersysteme | Diplomarbeit |
Björn Braun |
| Implementierung eines Kontaktmodells zur Simulation flächiger Reibkontakte | Masterarbeit |
Kai Becker |