Dipl.-Ing. Maxime Koebele
- Raum: 102
- Tel.: +49 721 608-41901
- Fax: +49 721 608-46070
- maxime koebele ∂does-not-exist.kit edu
Postanschrift:
Karlsruher Institut für Technologie
Institut für Technische Mechanik
Teilinstitut Dynamik/Mechatronik
Postfach 6980
76049 KarlsruheHaus- und Lieferanschrift:
KIT-Campus Süd
Institut für Technische Mechanik
Teilinstitut Dynamik/Mechatronik
Geb. 10.23, 2.OG
Kaiserstraße 10
76131 Karlsruhe
Stochastic Analysis of Geometric Mistuning in Radial Compressor
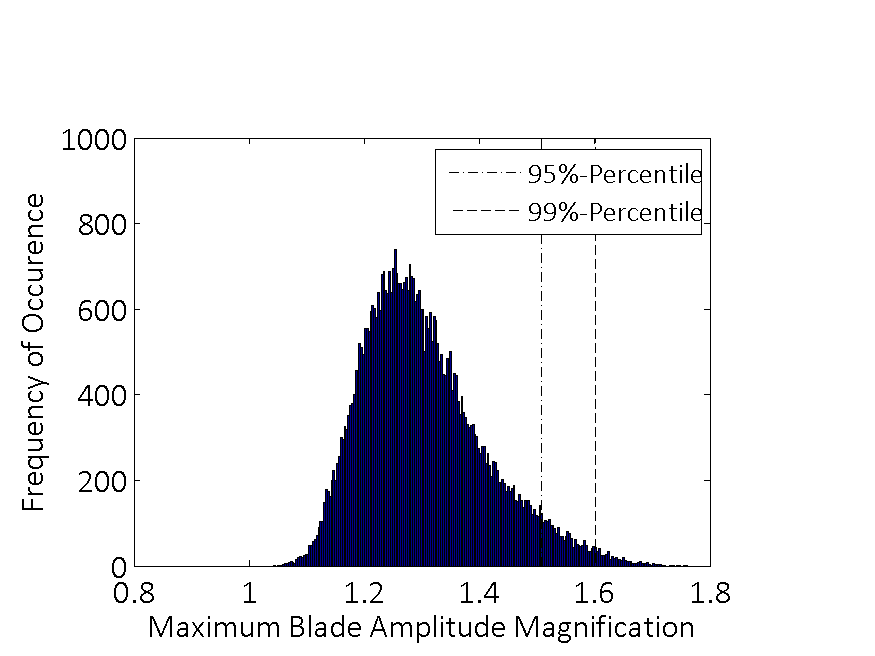
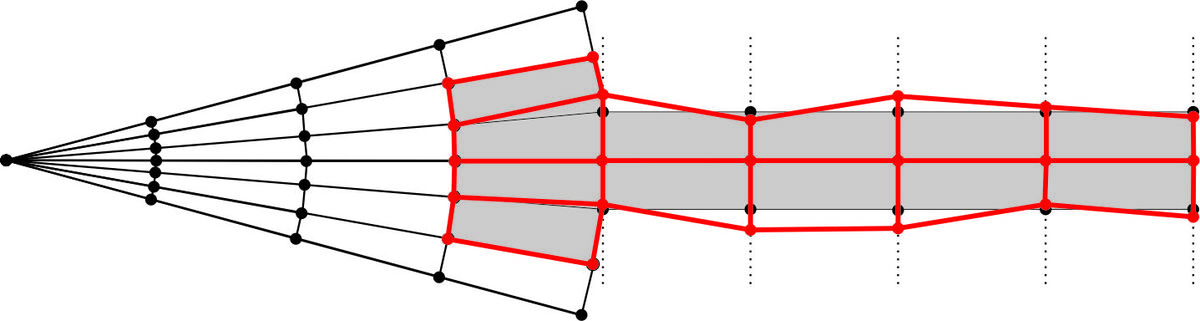
Radial compressor in turbochargers is often considered in theory as periodic system, but in fact it features inevitable small imperfections caused by material defects and manufacturing tolerances which break the cyclic periodicity. This is called mistuning. The loss of periodicity changes drastically the dynamic behavior of the compressor. Typically the forced response level of the mistuned bladed disk is larger than the tuned design. Because of the random nature of mistuning, the determination of the largest resonant response at any frequency has to be considered as a stochastic problem.
Mistuning receives significant attention from the research community since the late 1960s. Models using coupled lumped mass oscillators have allowed the fundamental phenomena of mistuning to be understood. More recently finite element model are used to explore with a better precision the behavior of mistuned compressor. To minimize the computational costs the finite element model has to be reduced first before performing a Monte Carlo Analysis. In the last decade several model reduction methods were developed. The way in which mistuning is implemented depends on the used reduction method and the vast part of them accounts only for a frequency mistuning model or a proportional mistuning model, in which the ideal tuned configuration is not modified.
Today a key topic is to combine this reduction methods with a more realistic introduction of mistuning, such as geometric mistuning. In other words, it will be tried to take directly random geometry modifications into consideration in a stochastic problem.
Contact: Prof. C. Proppe, M. Koebele
Publikationen
Koebele, M.; Proppe, C.
2017. Proceedings in applied mathematics and mechanics, 17 (1, SI), 723–724. doi:10.1002/pamm.201710330
Betreute Lehrveranstaltungen
| SS 19 | Übungen zu Maschinendynamik |
| WS 18/19 | Übungen zu Mathematische Methoden der Dynamik |
| SS 18 | Übung zu Maschinendynamik |
| WS 17/18 | Übungen zu Mathematische Methoden der Dynamik |
| SS 17 | Übungen zu Maschinendynamik |
| WS 16/17 | Übungen zu Mathematische Methoden der Dynamik |
| SS 16 | Übungen zu Maschinendynamik |
| WS 15/16 | Übungen zu Mathematische Methoden der Dynamik |
| SS 15 | Übungen zu Maschinendynamik |
| WS 14/15 | Übungen zu Mathematische Methoden der Dynamik |
| SS 14 | Übungen zu Maschinendynamik |
| WS 13/14 | Übungen zu Mathematische Methoden der Dynamik |