Dr.-Ing. Kai Becker
- Sprechstunden:
nach Vereinbarung
- Raum: 205.2
- Tel.: +49 721 608-46823
- Fax: +49 721 608-46070
- kai becker ∂does-not-exist.kit edu
Postanschrift:
Karlsruher Institut für Technologie
Institut für Technische Mechanik
Teilinstitut Dynamik/Mechatronik
Postfach 6980
76049 KarlsruheHaus- und Lieferanschrift:
KIT-Campus Süd
Institut für Technische Mechanik
Teilinstitut Dynamik/Mechatronik
Geb. 10.23, 2.OG
Kaiserstraße 10
76131 Karlsruhe
Research Topic: Journal Bearings with Variable Geometry
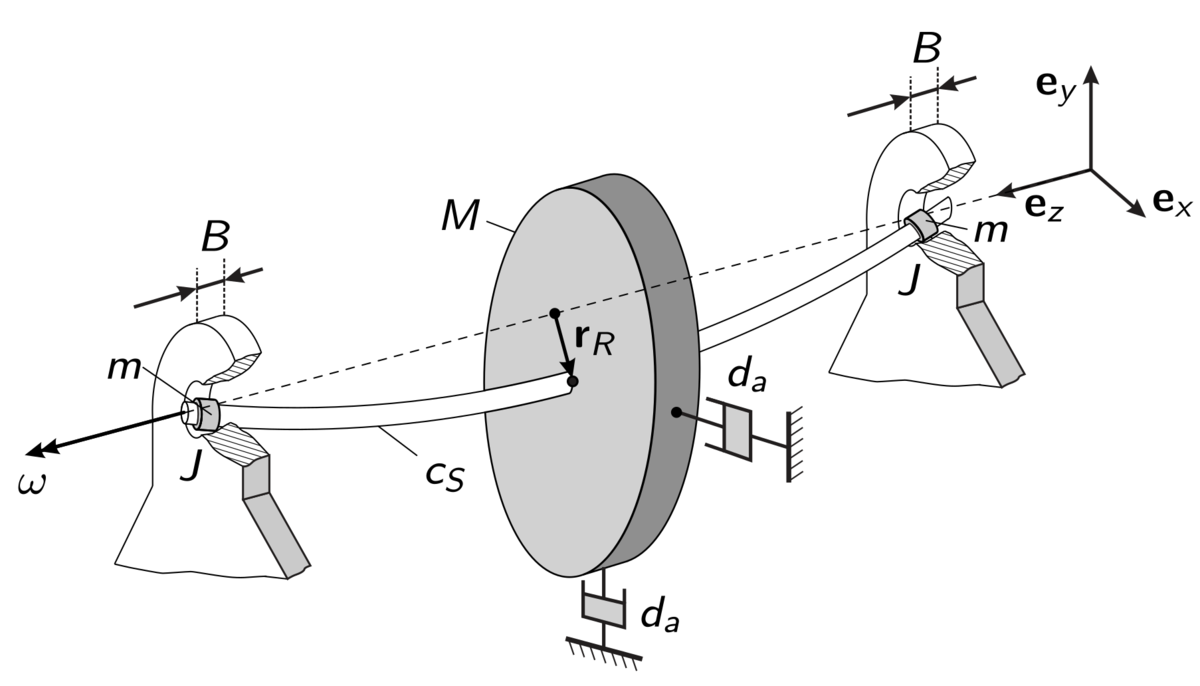
The improvement of rotordynamic systems being supported by oil-lubricated journal bearings represents an ongoing field of research.
As the rotational speed of the rotor system is increased, an instability can be detected which is often referred to as ‘oil-whirl’ or ‘half-frequency-whirling’ in literature. As the frequency of this ‘whirling’ instability meets an eigenfrequency of the associated elastic rotor, its oscillation amplitudes increase tremendously which is also known as ‘oil-whip’. These ‘oil-whirl’ and ‘oil-whip’ effects can be rated as rather critical and should be avoided during the operation of the rotor system.
Various modifications (compared to the ‘classical’ cylindrical bearing) have been proposed in literature in order to suppress or at least to decrease these unwanted effects.
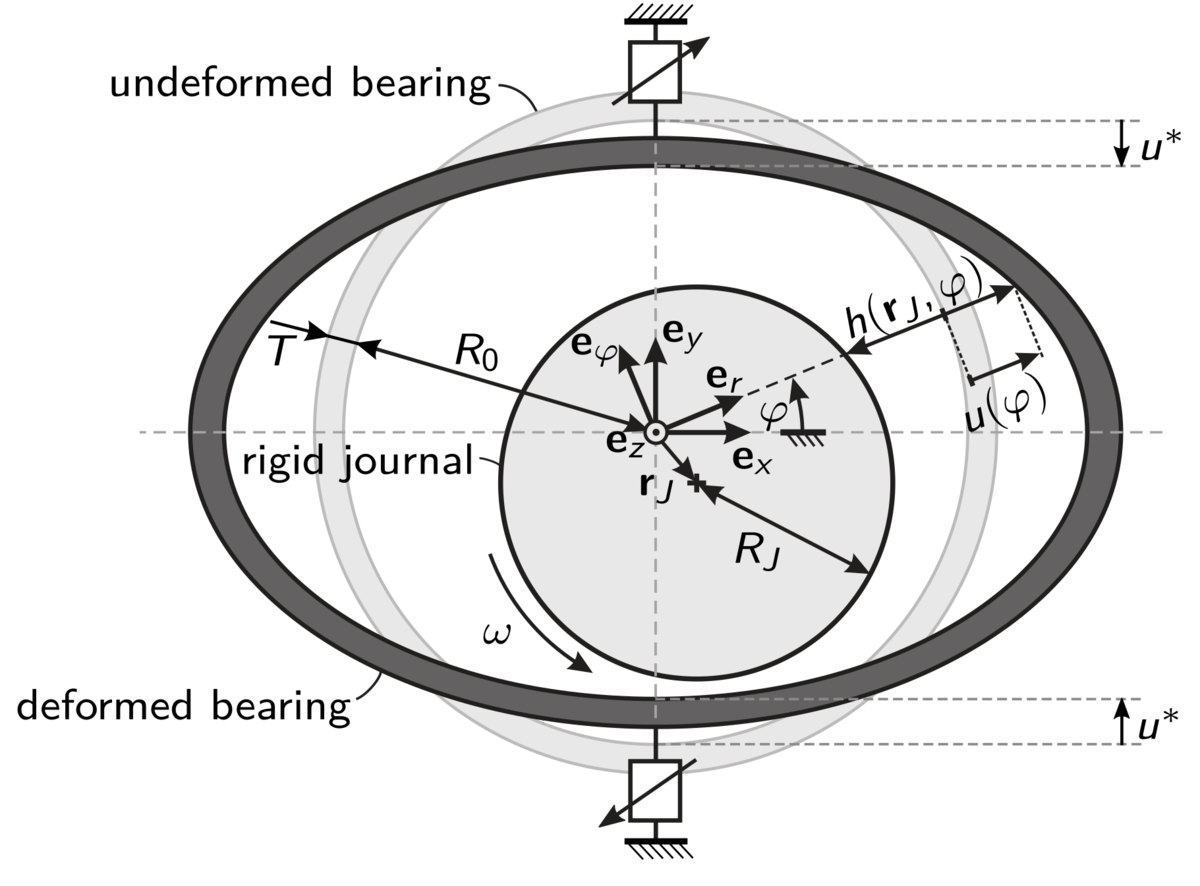
By applying a variable change in geometry of the supporting journal bearings, improvements of the rotor's dynamic behaviour are expected. Starting from an initially circular profile, the bearing is elastically deformed by an appropriate actuation mechanism which leads to a complex fluid-solid-interaction.
The effects of this change in geometry on the rotor system are studied by means of systematic stability and bifurcation analysis, focusing on time-efficient modelling methods.
Contact: Kai Becker, Seemann, Wolfgang
Publikationen
Becker, K. and Seemann, W. (2015),
A Journal Bearing with actively modified geometry for extending the parameter-based stability range of rotor dynamic systems
M07 Colloque EUROMECH Coupling and Nonlinear interactions in Rotating Machinery. AFM, Association Française de Mécanique, 2015.
Becker, K. and Seemann, W. (2016)
Approximation of quasi‐periodic solutions of a rotor in two‐lobe bearings with time‐varying geometry
PAMM, 16(1) (2016), 263-264.
DOI: 10.1002/pamm.201610120
Becker, K. and Seemann, W. (2016),
A Journal Bearing with actively modified geometry for extending the parameter-based stability range of rotor dynamic systems
International Symposium on Transport Phenomena and Dynamics of Rotating Machinery, 2016.
Betreute Lehrveranstaltungen
| WS 19/20 | Engineering Mechanics III (Tutorial) |
| SS 19 | Übungen zu 'Einführung in die Mehrkörperdynamik' |
| WS 18/19 | Übungen zu Technische Mechanik III |
| SS 18 | Übung zu Mathematische Methoden der Schwingungslehre |
| WS 17/18 | Übungen zu Einführung in nichtlineare Schwingungen |
| SS 17 | Workshop 'Arbeitstechniken im Maschinenbau' (ITM, Seemann) |
| WS 16/17 | Übungen zu Einführung in de Technische Mechanik II: Dynamik |
| SS 16 | Übungen zu Einführung in die Mehrkörperdynamik |
| WS 15/16 | Übungen zu Technische Mechanik III |
| WS 15/16 | Engineering Mechanics III (Tutorial) |
| SS 15 | Übungen zu Einführung in die Mehrkörperdynamik |
| WS 14/15 | Übungen zu Technische Mechanik III |
| WS 14/15 | Engineering Mechanics III (Tutorial) |