Dr.-Ing. Olga Drozdetskaya
- Sprechstunden:
nach Vereinbarung
- Raum: 101
- Tel.: +49 721 608-41899
- Fax: +49 721 608-46070
- olga drozdetskaya ∂does-not-exist.kit edu
Postanschrift:
Karlsruher Institut für Technologie
Institut für Technische Mechanik
Teilinstitut Dynamik/Mechatronik
Postfach 6980
76049 KarlsruheHaus- und Lieferanschrift:
KIT-Campus Süd
Institut für Technische Mechanik
Teilinstitut Dynamik/Mechatronik
Geb. 10.23, 2.OG
Kaiserstraße 10
76131 Karlsruhe
Research Topic: Self-balancing of the planetary moving rotor
The phenomenon of self-balancing of rigid rotors is well known and investigated for rotors with fixed bearings. However, in some technical devices the rotor performs complex motions. An example of such system is a computed tomography scanner. Its anode rotates very fast in the housing of the X-ray tube. At the same time the X-ray tube itself rotates rather slowly around the patient’s body. It is very important for CT scanner to keep the minimal possible level of vibrations in order to obtain good image quality. The objective is to investigate how and to which extent the self-balancing devices can be used for reducing vibrations in a planetary moving rotor.
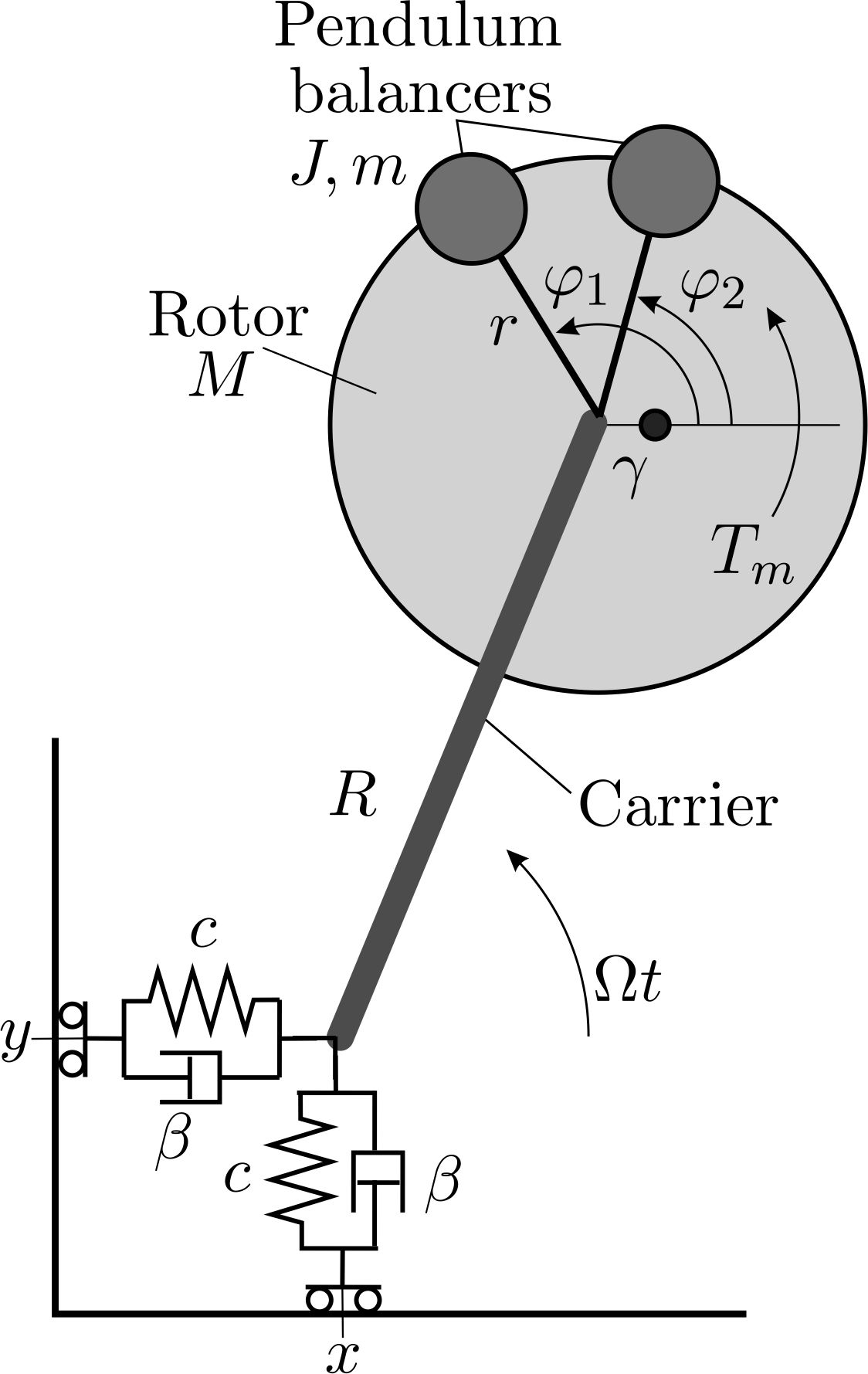
The model to consieder consists of the rotor of mass M, which is fixed on the end of the rigid carrier. The other end of the carrier is elastically suspended with radial spring-dampers of a certain stiffness c and damping b. The carrier rotates around it’s point of suspension with a constant velocity Ω. At the same time the rotor rotates around its symmetry axis with a given velocity ω. Its centre of mass has an offset relative to the rotation axis. Two pendulum balancers of mass m, moment of inertia J and length r are placed on the rotation axis of the rotor.
The stationary solutions of the system and the passage through the resonanceare are investigated analytically using averaging technique for the strongly damped systems. Analytic results match very well with numeric simulations when the velocity of the planetary motion is sufficiently small.
Contact: ,
Publikationen
Drozdetskaya, O.
2020, Dezember 16. Karlsruher Institut für Technologie (KIT). doi:10.5445/IR/1000127738
Jehle, G.; Drozdetskaya, O.; Fidlin, A.
2017. Contributions to the foundations of multidisciplinary research in mechanics : papers presented during the 24th International Congress of Theoretical and Applied Mechanics (ITCAM2016), Montreal, Canada, 22-26 August, 2016. Ed.: J.M. Floryan, 210–211, National Research Council Canada
Drozdetskaya, O.; Fidlin, A.
2017. 24th International Congress of Theoretical and Applied Mechanics (ICTAM) - Contributions to the Foundations of Multidisciplinary Research in Mechanics, Montreal, Canada, 21-26 August, 2016. Vol.: 1. Ed.: J. M. Floryan, 126–127, National Research Council Canada
Drozdetskaya, O.; Fidlin, A.
2018. European journal of mechanics / A, 72, 516–520. doi:10.1016/j.euromechsol.2018.05.018
Fidlin, A.; Drozdetskaya, O.
2016. Procedia IUTAM, 19, 43–52. doi:10.1016/j.piutam.2016.03.008
Drozdetskaya, O.; Fidlin, A.
2016. Procedia IUTAM, 19, 126–135. doi:10.1016/j.piutam.2016.03.017
Drozdetskaya, O.; Fidlin, A.; Waltersberger, B.
2011. Proceedings of the 7th European Nonlinear Dynamics Conference (ENOC 2011), Rome, Italy, July 24-29, 2011. Ed.: D. Bernardini, 6 S., Sapienza Università di Roma
Fidlin, A.; Drozdetskaya, O.
2011. Schwingungen in Antrieben 2011: 7. Fachtagung, Leonberg, 19. und 20. Oktober 2011, 183–194, VDI Verlag
Fidlin, A.; Drozdetskaya, O.; Waltersberger, B.
2011. European journal of mechanics / A, 30 (5), 665–672. doi:10.1016/j.euromechsol.2011.03.009
Betreute Lehrveranstaltungen
| SS 19 | Übungen zu Einführung in die Technische Mechanik I: Statik und Festigkeitslehre |
| WS 18/19 | Übungen zu Einführung in die nichtlinearen Schwingungen |
| SS 18 | Übung zu Stabilitätstheorie |
| WS 17/18 | Übungen zu Technische Schwingungslehre |
| SS 17 | Übungen zu Mathematische Methoden der Schwingungslehre |
| WS 16/17 | Übungen zu Dynamik des Kfz-Antriebsstrang |
| SS 16 | Übungen zu Einführung in die Technische Mechanik I |
| WS 15/16 | Übungen zu Stabilitätstheorie |
| SS 15 | Übungen zu Einführung in nichtlineare Schwingungen |