
Dr. Dipl.-Math. Yuriy Sinchuk
- Former Scientific Employee / Member of the Heisenberg-Group †
Karlsruher Institut für Technologie (KIT)
Kaiserstraße 10
Gebäude: 10.23
76131 Karlsruhe
Curriculum Vitae
| 09/1999 – 06/2004 | BSc, MSc in Informatics Department of Applied Mathematics and Informatics Ivan Franko L’viv State University, Ukraine Master thesis: An adaptive finite element method for convection-diffusion problems |
| 04/2004 – 03/2007 | Software Engineer in SoftServe, L’viv, Ukraine, Numerous object-oriented software development projects (mostly C++ source code, WIN32 applications |
| 11/2004 – 07/2009 | PhD Student, Teaching Assistant, Engineer, Laboratory Assistant Department of Applied Mathematics and Informatics Ivan Franko State University, L’viv, Ukraine PhD Thesis: “Adaptive schemes of finite elements method for singularly perturbed variation convection-diffusion problems” |
| 07/2009-01/2010 | Mathematician-Programmer TzOV “Mathematical Centre”, L’viv, Ukraine Project related to hydraulic net calculation of the gas-transport system (Delphi source code) |
| 02/2010- 11/2014 | Scientific Employee Institute of Engineering Mechanics Karlsruhe Institute of Technology (KIT) Research Work within the Heisenberg Group: “Microstructure modeling of the multiphase materials” |
Studies and Teachings at the Ivan Franko State University, L’viv, Ukraine
(Department of Applied Mathematics and Informatics)
Summer Term 2008
Workshop: Data bases and information systems
Workshop: Software of the computes
Workshop: Functional analyses in numerical mathematics
Winter Term 2005/2006
Workshop: Numerical practice
Research Subject
Microstructural modeling and optimization of metal matrix composites
Project:
Numerical microstructure optimization of melt-infiltrated metal-ceramic composites
Summary:
A numerical two-scale method for the microstructure optimization of microsamples and components made of melt-infiltrated metal-ceramic composite materials with maximum macroscopic stiffness under quasi-static mechanical loading is to be developed. The macroscopic modeling is carried out using the FE method. Each integration point in the element, which consists of several domains (of areas of the same orientation and geometry of the inclusions), represents the microstructure at the microlevel. The effective stiffness of the microstructure at the microlevel under the effect of the macroscopic distortions is determined using micromechanical two-step homogenization methods certainly. The inelastic material behavior of the individual material phases is taken into account incrementally by corresponding material laws when determining the tangent stiffness of the individual domain in the first homogenization step. The effective stiffness at the integration point is determined in the second homogenization step. The limitations on design variables of the optimization should be defined from the statistical studies of the microstructure and from knowledge of the manufacturing process. The optimization problem should be solved iteratively, first for a simple problem and then for a cap-shaped prosthesis. To determine the material laws for individual phases and to verify the microstructure modeling and optimization, numerous existing experimental data from studies of micro and macro samples as well as from FE models of the real microstructure are introduced.
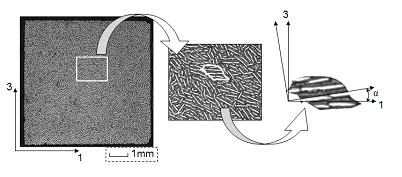
Typical microstructure of melt-infiltrated metal-ceramic composites (photographs by S. Roy IWK1)
Publications
In Books
Sinchuk Y., Piat R., Vasoya M.:
Elastic Properties of Metal-Ceramic Composites: Micromechanical Estimation and Microstructure.
In Ed: Krenkel W., Lamon J.: High Temperature Ceramic Materials and Composites, AVISO Verlagsgesellschaft mbH, Berlin, Germany,
228-233 (2010).
In Journals (Bold Roman: Referred Journal Article)*
2008
Sinchuk Y., Shynkarenko G. :
A posteriori error estimator of FEM approximation for convection-diffusion-reaction problem.
Journal of Ternopil State Tech. University. 13(2):169–174, 2008
Sinchuk Y. :
Adaptive scheme of finite elements method for singularly perturbed convection-diffusion problems.
Physic.-math. model. and information technologies., 7:95–102, 2008
2007
Sinchuk Y., Shynkarenko G.
Finite element method approximation with exponential weighting functions.
App. Problems Mech. Math. 5:61–70, 2007
Sinchuk Y., Shynkarenko G. :
Exponential discretization of the Cauchy problem for ordinary differential equations.
Physic.-math. model. and information technologies., 6:91–100, 2007
Sinchuk Y., Shynkarenko G. :
The exponential FEM approximations for singularly perturbed problems convection-diffusion-reaction.
Journal of Lviv University Series applied math. and inform., 12:112–121, 2007
